  |
|
|
|||||||||||||||||||||||||||
|
Построить овал можно двумя способами, в зависимости от изначально заданных параметров.
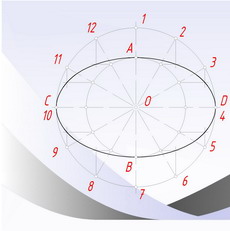
1 способ построения овала  3. Соединяем прямой линией точки С и В.  4. Из центра О соединяем горизонтальную и вертикальную ось радиусом ОВ (намечаем точку е)  5. Из точки С проводим дугу радиусом Се до пересечения с наклонной прямой СВ (намечаем точку f).  6. Участок между точками f и B наклонной прямой делим на две равные части. Для этого из точки f проводим дугу радиусом fВ, затем из точки В проводим дугу того же радиуса, до пересечения с дугой, построенной ранее.  7. Соединяем точки пересечения дуг. Эта линия будет являться перпендикуляром к отрезку fВ и будет делить его пополам. Отмечаем точки пересечения построенной линии с горизонтальной и вертикальной осями симетрии (l и k).  8. Строим точку m симметричную точке l.  9. Строим точку n симметричную точке k.  10. Из точки k проводим прямую через точку m. Из точки n проводим прямые мерез точки m и l.  11. Радиусом равным расстоянию kC из точки k проводим дугу, соединяющую наклонные линии, исходящие из точки k. Тем же радиусом из точки n, как из центра, проводим дугу соединяющую наклонные линии исходящие из точки n. 12. Из точек m и l, как из центров, проводим дуги радиусом mA и замыкаем ими ранее проведенные дуги.  На этом построение овала можно считать занонченным.
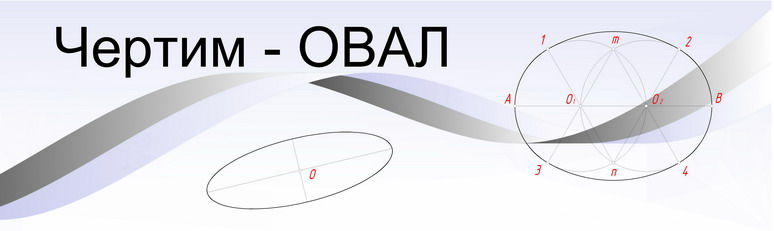
2 способ построения овала  2. Радиусом, равным расстоянию О1О2, из точек деления О1 и О2 проводим окружности. Точки пересечения окружностей обозначаем как m и n.  3. Соединяем точки m и n с точками О1 и О2 получаем прямые, которые продляем до пересечения с окружностями. Полученные точки (1,2,3 и 4) являются точками сопряжениями дуг.  4. Из точек m и n, как из центров, радиусом Rmax, равным n 2 и m 3, проводим верхнюю дугу 1 2 и нижнюю дугу 3 4.  На этом построение овала можно считать занонченным. |
||||||||||||||||||||||||||||

|
|
|
