  |
|
|
|||||||||||||||||||||||||||
|
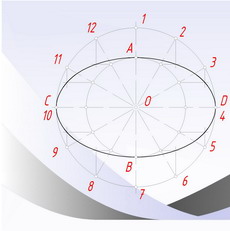
Эллипс - замкнутая плоская кривая, сумма расстояний каждой точки которой до двух данных точек (фокусов), лежащих на большой оси, есть величина постоянная и равная длине большой оси. Широко применяемый в начертательной геометрии способ построения эллипса по большой (СD) и малой (АВ) осям мы рассмотром в этом разделе. 1. Проводим центровые линии. Чертим из одной точки две окружности.  2. Диаметр меньшей окружности равен заданной ширине эллипса (малой оси АВ), диаметр большей - длине эллипса (большей оси СD).  3. Делим большую окружность на двенадцать равных частей. Точки делений соединяем прямыми линиями, проходящими через центр О. Эти прямые разделят меньшую окружность тоже на двенадцать равных частей.  4. Из точек делений на большей окружности (за исключением точек 1,4,7 и 10) проводим вертикальные линии.  5. Из точек делений на меньшей окружности (за исключением точек А и В проводим горизонтальные линии, пересекающиеся с соответствующими им по номерам вертикальными линиями.  6. Точки пересечений вертикальных и горизонтальных линий, а также точки А, В, С и D соединяем плавной кривой, которая образует эллипс.  На этом вычерчивание эллипса считаем законченным. Хотя эллипс и похож на овал, он не являестя овалом. Эллипс относится к лекальным кривым. |
||||||||||||||||||||||||||||

|
|
|
